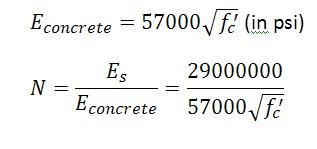In this section, we're discussing the behavior and basics of reinforced concrete under loads. We'll also discuss designing a member by varying the cross sectional area and the amount of reinforcement. I'll use ACI 318 equations and provisions. This is what I want to talk about:
- Concrete structural
- Flexure Analysis
- Singly reinforced beam
- Doubly reinforced beam
- T beam
- Flexure Design
- Shear
- Bond Development
- Combined loading (Columns)
Concrete Structural Properties
Concrete is a material used for its compressive strength. The point of reinforcing a concrete member is to allow the reinforcement assume tensile requirements in a member, limit cracking and confine the core (shear and torsion). I'll explain these phenomena when necessary.
We denote the compressive strength of concrete by (f'c) which can range anywhere from 2000 psi to 10000+psi (or 2ksi to 10 ksi). We'll also use the notation (fy) for the yield strength of steel, which is 60000 psi or 60 ksi. Lets pretend we have a little reinforced column that we want to crush, we have to add the strength of the reinforcement to the concrete strength. All we do is compare a ratio of the steel's elasticity modulus to the concrete modulus and make an equivalent section:
- Where N is the ratio of the moduli of elasticity (concrete vs. steel). N is usually 8.
Lets also talk about the modulus of rupture (fr), this is, essentially, the tensile strength of concrete. When the modulus of rupture is reached in the extreme tensile face of a concrete member, the member cracks. If the member is not reinforced, it will crack through the cross section and cause failure. If the beam is reinforced, the crack will propagate to the neutral axis of the equivalent cracked section. The moment that causes cracking is called the cracking moment. Look:
If (usually) the beam is found to be cracked follow the below procedure to determine the neutral axis (kd).
Flexure
Since concrete has such a low tensile capacity (strength), it permissible to neglect any tensile resistance in a member. That means, for a concrete member in flexure, the capacity is dependent on the moment created by the couple (forces acting in opposite directions with a distance between them) of the concrete in compression and the reinforcement in tension.
So, what are the allowable values for concrete and the reduction safety factors? Well, ACI 318 only allows for concrete calculations to use 85% of the actual concrete strength (.85f'c). However analyze a members moment capacity based off the yield strength of the reinforcement bars. For tension controlled sections the reduction factor (phi) = .9. Note that the term ( B1) is used, its value is .85 for a concrete strength of .85 and reduces by .05 for ever increase of 1000 psi.
Singly reinforced Beam Analysis
To analyze a singly reinforced beam's flexural capacity (Mn), use the following process:
Doubly Reinforced Beam Analysis
To analyze doubly reinforced beams, use the following procedure:
Singly reinforced Beam Analysis
To analyze a singly reinforced beam's flexural capacity (Mn), use the following process:
Flexure Analysis
To analyze doubly reinforced beams, use the following procedure:
T-Beam Analysis
Flexure Design
I've already introduced the important concepts regarding strength reduction (safety, phi) factors in the previous section. Design is an iterative process, keep this in mind. If you first don't succeed, try bigger values (b and d). Check out this guide for singly reinforced beam design:
I've already introduced the important concepts regarding strength reduction (safety, phi) factors in the previous section. Design is an iterative process, keep this in mind. If you first don't succeed, try bigger values (b and d). Check out this guide for singly reinforced beam design:
- Note that a phi value of .9 is used because the section is designed to be tension controlled. This means that the tension reinforcement yields before the concrete crushes.
So, I've covered two main topics in flexure design. Doubly reinforced beam design is very tedious and complicated, and usually involves many iterations to meet ACI specifications. I could have also included slab and doubly reinforced T-Beam design, however, one way slab design is really easy (it is similar to singly reinforced flexure design). I will likely include these in the future. If there is any other flexure topics you would like me to cover, feel free to ask.
Shear
Shear is a completely new topic. Shear capacity of a member is dependent on the shear capacity of the beam's cross section. The capacity of the cross section to handle design shear may not be sufficient. For this reason we may need shear reinforcement. Shear reinforcement maintains the homogeneity of a member by stopping shear cracks from propagating through a large amount of the beam.
The shear capacity (Vc) of a cross section is dependent on the cross-section's area and the tensile capacity of a beam (related to √f'c). The shear capacity is ultimately based on experimental results, the best fit equation for shear capacity and the design equation are:
For a member experiencing compression, use:
Here is the shear design procedure in accordance with ACI provisions:
Bond development
This has nothing to do with James Bond, although I've been told I look a lot like Pierce Brosnan. Jus seeing if you were paying attention! haha. Bond Development is my favorite topic in concrete mechanics. It may seem a bit abstract at first, but you'll see how cool it is once I go into detail. So, what is bond? Well, if we want to get all the moment capacity we've been calculating in the previous sections we need to ensure that there is enough length and "friction" (bond) between the reinforcing bars and the concrete.
At the end of the day we need a certain length of bar past our critical point (the place of maximum moment, and, thus the maximum force being applied to the rebar). This is called the development length, and it is a function of the concrete tensile strength, rebar yield strength, rebar coating (epoxy), concrete cover, spacing, transverse reinforcement, and reinforcement placement. Yes, this equation is going to get complicated quick, remember, it is just an equation. Here is the mega bond development equation (discovered from our very own, University of Kansas!):
This has nothing to do with James Bond, although I've been told I look a lot like Pierce Brosnan. Jus seeing if you were paying attention! haha. Bond Development is my favorite topic in concrete mechanics. It may seem a bit abstract at first, but you'll see how cool it is once I go into detail. So, what is bond? Well, if we want to get all the moment capacity we've been calculating in the previous sections we need to ensure that there is enough length and "friction" (bond) between the reinforcing bars and the concrete.
At the end of the day we need a certain length of bar past our critical point (the place of maximum moment, and, thus the maximum force being applied to the rebar). This is called the development length, and it is a function of the concrete tensile strength, rebar yield strength, rebar coating (epoxy), concrete cover, spacing, transverse reinforcement, and reinforcement placement. Yes, this equation is going to get complicated quick, remember, it is just an equation. Here is the mega bond development equation (discovered from our very own, University of Kansas!):
The bond development equation is pretty cool, but how does one apply it? Well, this is where you have to be familiar with the ACI Code. In the code there is a great illustration in section 12, the bond section, that shows you everything you need to know about development lengths. There are a ton of bond provisions and requirements to be made, reference the code when in question.
A lot of the time there is not enough room in a structure to implement the entire development length, this is why hooks were developed. Simply put, a hook has a shorter bond development length; this is its advantage. The two most common hooks are the 90 degree and 180 degree hooks, here are the code provisions for bend diameters and development lengths:
There really is a ton to talk about in bond development. Without getting into super ACI provisional talk, I hope I gave you a gist of what is going on with bond development. The best thing you can do with regards to learning bond development is getting to know ACI 318 section 12.
Combined loading (Columns)
Combined loading is the situation in which a member is experiencing axial (compression) loading and bending. This situation is pretty neat, remember how concrete preforms poorly in tension? The following diagram explains how a a column functions under combing loading:
The above diagram demonstrates how a compressive axial force adds only compressive stress to the column. The non-linear behavior of concrete benefits from this phenomena because the axial force shifts the neutral axis up, which allows more concrete to be in compression and reduces the reinforcement tensile stress. Lets look at the design axial force for a short column:
Combined loading is the situation in which a member is experiencing axial (compression) loading and bending. This situation is pretty neat, remember how concrete preforms poorly in tension? The following diagram explains how a a column functions under combing loading:
The above diagram demonstrates how a compressive axial force adds only compressive stress to the column. The non-linear behavior of concrete benefits from this phenomena because the axial force shifts the neutral axis up, which allows more concrete to be in compression and reduces the reinforcement tensile stress. Lets look at the design axial force for a short column:
- This example is obvious, of course the design axial capacity is going to be dependent on the are of reinforcement and the concrete area (along with the reduction factors).
- The chart is clearly labeled to describe the states of the reinforcement in the column. At the top, where the axial load is the greatest and there is little bending, all reinforcement is experiencing compression. Zone 2 is a transition zone where the tensile steel is at less that half the yield strength. In zone 3, the tensile steel is under high stress.
Summary
I realize there is a ton of information to be said about basic concrete design, but I've tried to supplement you learning with some examples and procedures. I hope this has served as an aid to your studies. If you have any questions or think there is something for me to add, feel free to email me.
I realize there is a ton of information to be said about basic concrete design, but I've tried to supplement you learning with some examples and procedures. I hope this has served as an aid to your studies. If you have any questions or think there is something for me to add, feel free to email me.